Distribución Normal
La Distribución Normal:
Fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la "campana de Gauss". La distribución normal es un modelo teórico capaz de aproximar satisfactoriamente el valor de una variable aleatoria a una situación ideal. En otras palabras, la distribución normal adapta una variable aleatoria a una función que depende de la media y la desviación típica. Es decir, la función y la variable aleatoria tendrán la misma representación pero con ligeras diferencias.
La distribución de una variable normal está completamente determinada por dos parámetros, su media y su desviación estándar, denotadas generalmente por y . Con esta notación, la densidad de la normal viene dada por la ecuación:
Ecuación 1: |
|
Que determina la curva en forma de campana que tan bien conocemos. Así, se dice que una característica X sigue una distribución normal de media ![]() y varianza
y varianza ![]() , y se denota como
, y se denota como![]() , si su función de densidad viene dada por la Ecuación 1.
, si su función de densidad viene dada por la Ecuación 1.
Al igual que ocurría con un histograma, en el que el área de cada rectángulo es proporcional al número de datos en el rango de valores correspondiente si, en el eje horizontal se levantan perpendiculares en dos puntos a y b, el área bajo la curva delimitada por esas líneas indica la probabilidad de que la variable de interés, X, tome un valor cualquiera en ese intervalo. Puesto que la curva alcanza su mayor altura en torno a la media, mientras que sus "ramas" se extienden asintóticamente hacia los ejes, cuando una variable siga una distribución normal, será mucho más probable observar un dato cercano al valor medio que uno que se encuentre muy alejado de éste.
Una variable aleatoria continua puede tomar cualquier número real. Por ejemplo, las rentabilidades de las acciones, los resultados de un examen, el coeficiente de inteligencia IQ y los errores estándar son variables aleatorias continuas.
Una variable aleatoria discreta toma valores naturales. Por ejemplo, el número de estudiantes en una universidad.
La distribución normal es la base de otras distribuciones como la distribución t de Student, distribución ji-cuadrada, distribución F de Fisher y otras distribuciones. Una de las distribuciones teóricas mejor estudiadas en los textos de bioestadística y más utilizada en la práctica es la distribución normal, también llamada distribución gaussiana. Su importancia se debe fundamentalmente a la frecuencia con la que distintas variables asociadas a fenómenos naturales y cotidianos siguen, aproximadamente, esta distribución. Caracteres morfológicos (como la talla o el peso), o psicológicos (como el cociente intelectual) son ejemplos de variables de las que frecuentemente se asume que siguen una distribución normal. No obstante, y aunque algunos autores, han señalado que el comportamiento de muchos parámetros en el campo de la salud puede ser descrito mediante una distribución normal, puede resultar incluso poco frecuente encontrar variables que se ajusten a este tipo de comportamiento.
Su importancia se debe a tres razones fundamentales:
Por un lado un gran número de fenómenos reales se pueden modelizar con esta distribución (tales el caso de las características cuantitativas de casi todas las grandes poblaciones). Por otro lado, muchas de las distribuciones de uso frecuente tienden a aproximarse a la distribución normal bajo ciertas condiciones; y, por último, en virtud del Teorema Central del Límite, todas aquellas variables que puedan considerarse causadas por un gran número de pequeños efectos (como pueden ser los errores de observación) tienden a distribuirse con una distribución normal.
Características de una Distribución Normal:
* Tiene forma de campana.
* Puede tomar cualquier valor (de menos infinito a más infinito),es decir, utiliza variables cuantitativas continuas.
* Es simétrica.
* La Media se sitúa en el centro de la Distribución Normal (en el punto máximo de la campana) y divide la campana en dos partes iguales.
* En esa distribución de probabilidad, la Media Aritmética, la Mediana y la Moda son iguales
* El área bajo la curva suma 1. (0.5 del lado izquierdo y 0.5 del lado derecho con respecto a la media).
* El área encerrada bajo la curva equivale a la probabilidad buscada (o al porcentaje de la población si multiplicamos por 100).
* La curva normal es asintótica, esto significa que se acerca cada vez más al eje de las X pero no llega a tocarla, por lo que se extiende de forma indefinida en ambos lados.
* Para definir que una variable sigue una distribución normal con una Media y una Desviación Estándar, se usa la siguiente expresión:
Como habíamos comentado, son muchos los casos de la vida real que se comportan como una distribución normal y calcular el área bajo la curva para cada distribución resultaría tediosa y complicada.
Para resolver este problema, todas las distribuciones normales se convierten a una distribución estándar normal.
¿Y cómo se hace? Lo primero que tenemos que hacer es calcular el estadístico Z que se obtiene restando: el dato de la variable menos la Media y dividiendo la diferencia entre la desviación estándar.
La mecánica de los gases de Maxwell:
Fue la obra del astrónomo Quetelet (más abajo) quien puso a James Clerk Maxwell (1831-1879) en el camino de la mecánica estadística: las moléculas de un gas son como los individuos de una población, ya que el desorden a escala individual se transforma en orden a escala poblacional.
Lo que importa de los movimientos de las partículas de gas, afirmó Maxwell, son dos cosas: la velocidad media a la que se mueve cada partícula la cual determina su energía cinética media y cuánto se aparta de esa media por arriba o por abajo. Maxwell intuyó que la distribución de velocidades semeja el tipo de curva en forma de campana. La curva de Maxwell indica cuántas partículas de gas se mueven a una velocidad determinada y se eleva suavemente desde velocidades bajas, alcanza el pico en la media, y vuelve a descender suavemente hacia las velocidades altas. Esta distribución muestra que muy pocas partículas alcanzan velocidades mucho más altas que el promedio. Maxwell dijo que lo importante no es la trayectoria precisa de todas las partículas del gas, sino su comportamiento medio. Maxwell imaginó un enjambre de abejas: las abejas zumban furiosamente en todas direcciones, pero el propio enjambre se mantiene estacionario, porque, teniendo en cuenta el promedio de sus vuelos, no es más probable que las abejas vuelen en una dirección que en otra. (Ball 2004)
La curva de Maxwell indica cuántas partículas de gas se mueven a una velocidad determinada y se eleva suavemente desde velocidades bajas, alcanza el pico en la media, y vuelve a descender suavemente hacia las velocidades altas. Esta distribución muestra que la mayoría de las partículas se mueven a una velocidad alrededor del promedio.
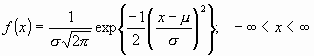





Comentarios
Publicar un comentario